3个大一高数第一章思维导图合集,内容涵盖1. 函数及其表示方法、2. 常见函数类型、3. 函数的运算、4. 函数的性质、5. 极限与连续等7个部分,每张思维导图都非常清晰,每张图片均值得收藏。
第1张,大一高数第一章思维导图附下载
第2张,大一高数第一章思维导图高清晰可打印
第3张,大一高数第一章思维导图高清晰可打印
第4张,大一高数第一章思维导图可打印
思维导图知识点说明:
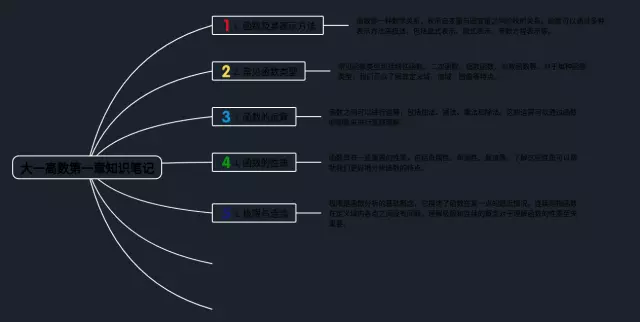
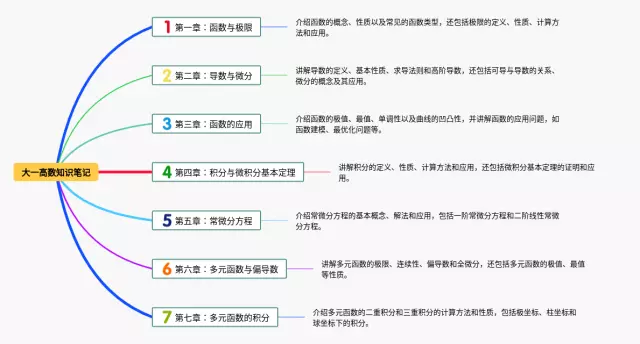
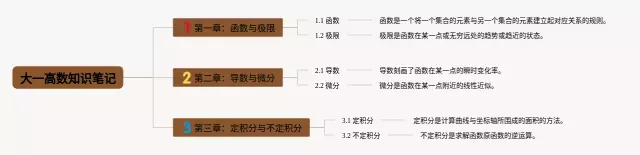
- 1. 函数及其表示方法:函数是一种数学关系,表示自变量与因变量之间的映射关系。函数可以通过多种表示方法来描述,包括显式表示、隐式表示、参数方程表示等。
- 2. 常见函数类型:常见函数类型包括线性函数、二次函数、指数函数、对数函数等。对于每种函数类型,我们可以了解其定义域、值域、图像等特点。
- 3. 函数的运算:函数之间可以进行运算,包括加法、减法、乘法和除法。这些运算可以通过函数的图像来进行直观理解。
- 4. 函数的性质:函数具有一些重要的性质,包括奇偶性、单调性、最值等。了解这些性质可以帮助我们更好地分析函数的特点。
- 5. 极限与连续:极限是函数分析的基础概念,它描述了函数在某一点的趋近情况。连续则指函数在定义域内各点之间没有间断。理解极限和连续的概念对于理解函数的性质至关重要。
- 6. 导数与微分:导数是描述函数变化率的工具,它定义了函数在某一点的切线斜率。微分则是导数的应用,它描述了函数在某一点的微小变化。
- 7. 高阶导数与泰勒展开:高阶导数用于描述函数变化的更细节特征,泰勒展开则可以用多项式逼近函数的近似值。掌握高阶导数和泰勒展开的方法可以更深入地理解函数的行为。


Comments (0)