4张勾股定理的思维导图 初二汇总,内容涵盖1、勾股定理、勾股定理的证明、3、勾股定理的适用范围、勾股数、勾股定理的逆定理等5个知识点,每张思维导图都非常简单,每张图片均可下载。
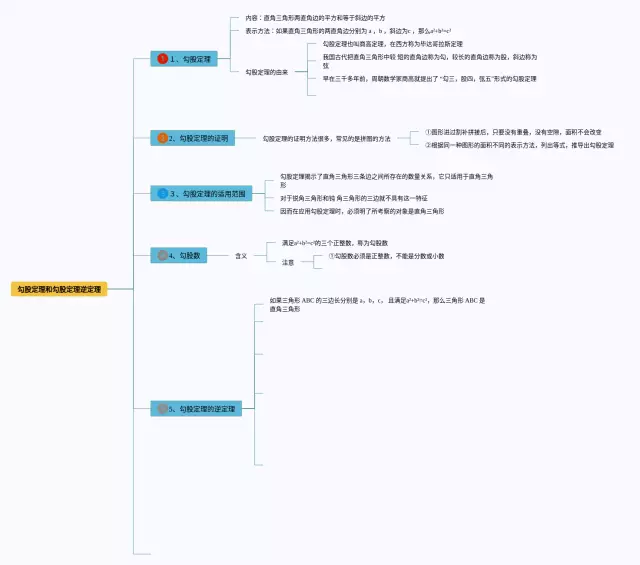
第1张,初二勾股定理的 思维导图高清版
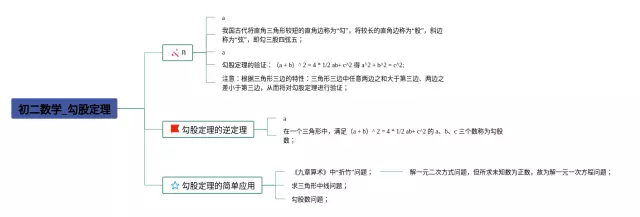
第2张,初二勾股定理的 思维导图附下载
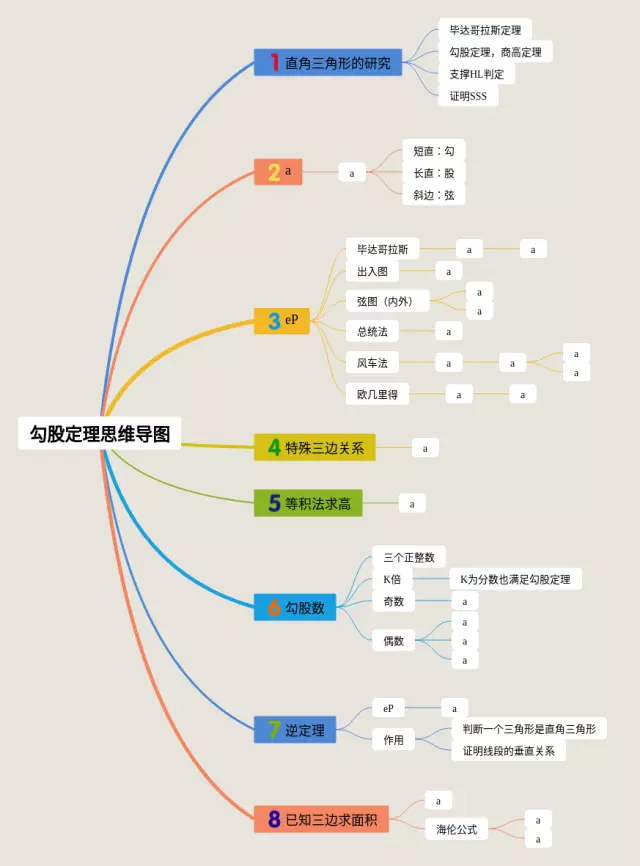
第3张,初二勾股定理的 思维导图附下载
第4张,初二勾股定理的 思维导图可打印
思维导图知识点说明:
- 1、勾股定理:内容:直角三角形两直角边的平方和等于斜边的平方
- 勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理
- 勾股定理的证明:
- 勾股定理的证明方法很多常见的是拼图的方法:①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变
- 3、勾股定理的适用范围:勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形
- 勾股数:
- 含义:满足a²+b²=c²的三个正整数,称为勾股数
- 勾股定理的逆定理:如果三角形 ABC 的三边长分别是 a,b,c, 且满足a²+b²=c²,那么三角形 ABC 是直角三角形
- 该定理在应用时要注意处理好如下几个要点:① 已知的条件:某三角形的三条边的长度
- 数形结合:最大边的平方<最小边的平方+中间边的平方:是锐角三角形
- 说明:勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法
- 勾股定理与勾股定理逆定理的区别与联系:区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理


Comments (0)